Creating Conic Curves

This task shows the various methods for creating conics, that is curves defined by five constraints: start and end points, passing points or tangents. The resulting curves are arcs of either parabolas, hyperbolas or ellipses.
The different elements necessary to define these curves are either:
  • two points, start and end tangents, and a parameter
  • two points, start and end tangents, and a passing point
  • two points, a tangent intersection point, and a parameter
  • two points, a tangent intersection point, and a passing point
  • four points and a tangent
  • five points.

Open the Conic1.CATPart document.

  1. Click Conic .

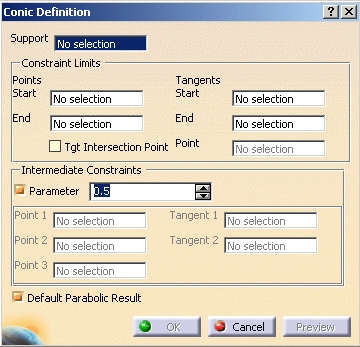
    The Conic Definition dialog box opens.

  2. Select the Support, that is the plane on which the resulting curve will lie.

  3. Fill in the conic curve parameters, depending on the type of curve to be created by selecting geometric elements (points, lines, etc.).

    Constraint Limits:
    • Start and End points: the curve is defined from the starting point to the end point
    • Tangents Start and End: if necessary, the tangent at the starting or end point defined by selecting a line
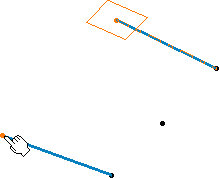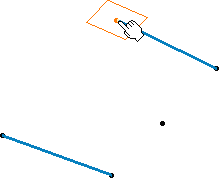
    Selecting the support plane and starting point Selecting the ending point
       
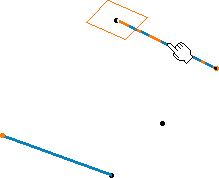
    Selecting the tangent at the starting point Selecting the tangent at the ending point
     
    Resulting conic curve
     
    • Tgt Intersection Point: a point used to define directly both tangents from the start and end point. These tangents are created on the virtual lines passing through the start (end) point and the selected point.
    Using a tangent intersection point Resulting conic curve
     

    Intermediate Constraints
    • Point 1, 2, 3: possible passing points for the curve. These points have to be selected in logical order, that is the curve will pass through the start point, then through Point 1, Point 2, Point 3 and the end point.
      Depending on the type of curve, not all three points have to be selected.
      You can define tangents on Point 1 and Point 2 (Tangent 1 or 2).
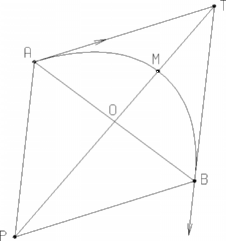
    • Parameter: ratio ranging from 0 to 1 (excluded), this value is used to define a passing point (M in the figure below) and corresponds to the OM distance/OT distance.
      If parameter = 0.5, the resulting curve is a parabola
      If 0 < parameter < 0.5, the resulting curve is an arc of ellipse,
      If 1 > parameter > 0.5, the resulting curve is a hyperbola.
    •  

  4. Clear Default Parabolic Result (it is selected by default), if you do not want the resulting conic curve to be parabolic.

  5. Click OK to create the conic curve.

    The conic curve (identified as Conic.xxx) is added to the specification tree.