Discretizing Curves


 This task shows you how to create a scan by sampling positions on a curve, according to the discretization mode you have selected.
The input can be curves or edges of surfaces.
The output is a V5 feature. It is automatically updated when the input is modified.
Open CurvetoScan01.CATPart from the samples directory.

  1. Make Geometrical Set.1 the Define in Work Object.

  2. Click Discretize Curves .
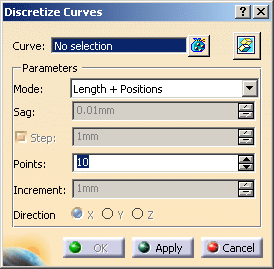
    The Discretize Curves dialog box is displayed:

  3. Select the curve to process (3D Curve.1).
    Multi-selection is available.
    is available to hide or show the selection.

  4. Select a discretization mode from the Mode drop-down list:

  5. Key-in the parameters requested by the mode you have selected.

  6. Click Apply to visualize the result and OK to validate and exit the dialog box.
    A Discretize Curves.1 feature is created in the Define in Work Object.

Modes and Parameters

In the examples below, the input curve looks like this:

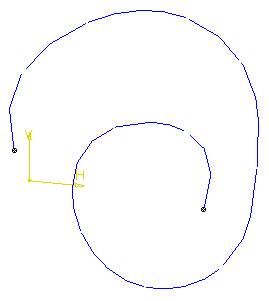
When selected, its color is orange. The scan is displayed in black.

Chord

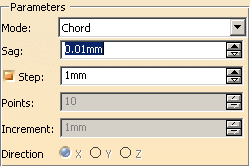
Sag:
Represents the maximum distance between the input curve and the theoretical chord connecting two successive positions of the scan.

Step:
Optional. Represents the maximum distance between two successive positions of the scan.

Examples:

Sag=0.1 mm, no step

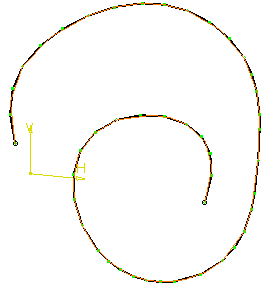
Sag=10 mm, no step

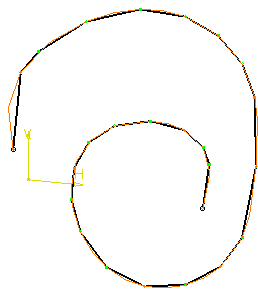
Sag=10 mm, Step=1 mm

Length + Positions

Points:
Is the number of positions N. The length of the curve is divided by (N-1, providing a constant curve-length increment.

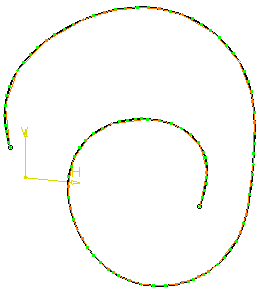
Example: Points=15

 

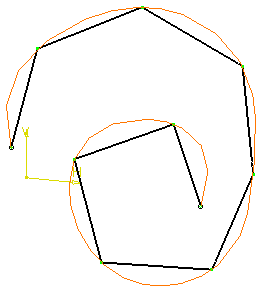
Length + Increment

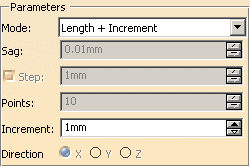
Increment:
Represents the length increment on the curve.

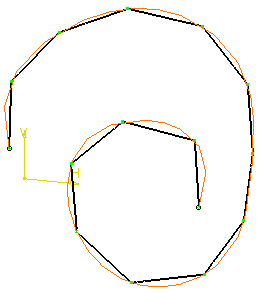
Example: Increment = 10 mm

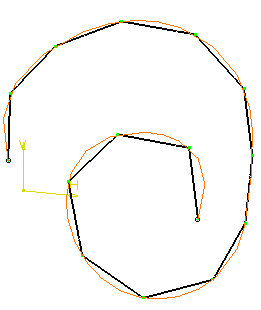
Parameter + Positions

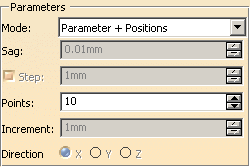
Points:
Is the number of positions N. The parameter of the curve is divided by (N-1), providing a constant curve-parameter increment.

Example: Points = 15

Direction + Increment

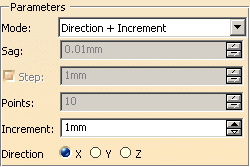
You must specify a main direction (x, y or z) in order to define a reference plane.
The origin of the reference plane is (0, 0, 0).

Increment:
This is the distance between two consecutive planes. Points are the result of the intersection of the planes with the curve.

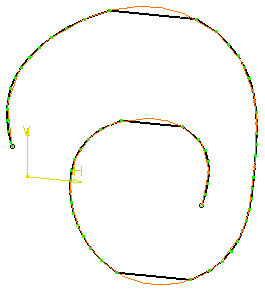
Example: Direction Y, Increment=1 mm